When we need to purchase a gas compressor, how do we determine the power it requires? Usually, we refer to the parameters provided by the manufacturer to get an approximate figure. However, instead of leaving the manufacturer in full charge, we can use the following formula to calculate the required power according to the gas source and the operating conditions of the equipment. It will facilitate us to get a better communication result with the manufacturer.
General calculation formula for power of the compressor
For a single compression stage, the power of the compressor required for isentropic compression is as follows.
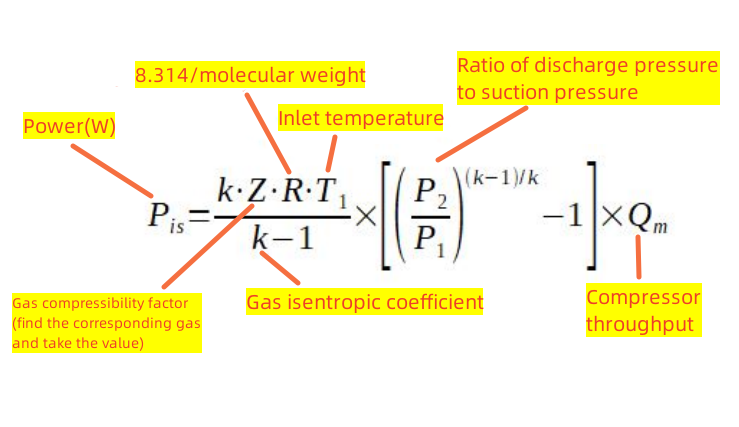
*Isentropic compression: Compression in which there is no friction, no internal leakage, and no heat exchange with the outside is called isentropic compression. In practice, we have to consider the compressor’s efficiency and correct the calculations with an efficiency factor (η). The manufacturer should provide the efficiency factor.
It is important to note that to calculate the power, we need to provide the following variables: the inlet temperature of the gas, the inlet and discharge pressures, and the flow rate of the gas. The energy required by the compressor is closely related to them. Several other essential constants: k refers to the isentropic coefficient of the gas, R refers to the gas constant/molecular weight, and Z refers to the compression coefficient of the gas, and you can look them up on the web or in an engineer’s manual.
For example, air’s k (isentropic coefficient) is 1.4, Z (compression coefficient) is 1 in the ideal case, and the molecular weight is 29, so R is 8.314/29. Carbon dioxide has a k (isentropic coefficient) of 1.28, a Z (compression coefficient) of 1 in the ideal case, and a molecular weight of 44, so R is 8.314/44.
Another thing to note is that the throughput needs to be converted from volume flow to mass flow before substituting it into the equation. Under standard conditions (i.e., 0°C and atmospheric pressure(101325pa)), the mass density of a gas is determined by the molar mass. You can check it just as quickly.
Simplified formula for power of the compressor
We can use a simplified formula for the isentropic compression of an ideal gas:
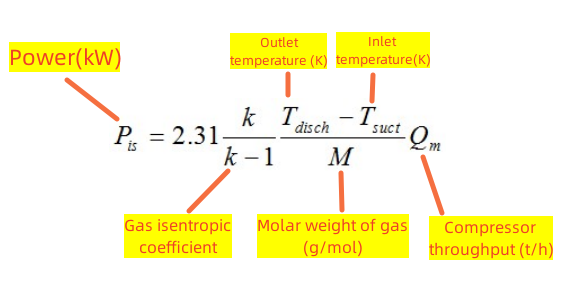
*An ideal gas: A gas that strictly obeys the experimental laws of gases at any temperature and pressure is called a perfect gas. Actual gases, especially those that do not liquefy quickly, such as hydrogen, oxygen, nitrogen, helium, etc., can be approximated as ideal gases when the pressure is not too high (not more than a few times the atmospheric pressure). The temperature is not too low (not less than negative tens of degrees Celsius).
How did we get this formula? Let’s explain it step by step.
Let’s start with the general formula:
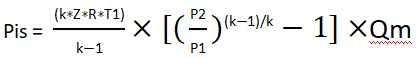
In the simplified formula, we assume that Z is 1(as an ideal gas), while R (gas constant/molecular weight) = 8.314/M
After substitution, we arrive at:
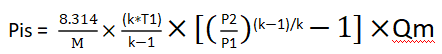
On the other hand, in isentropic compression, pressure changes and temperature changes can be related by the isentropic coefficient k,by the following formula:
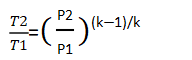
*T2 is outlet temperature and T1 is inlet temperature.
Replacing again, we get:
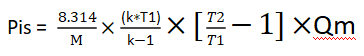
It can be simplified as follows:
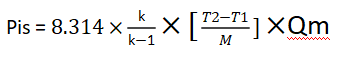
Finally, we need to note that the simplified formula is based on t/h, while the general formula considers kg/s:
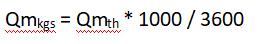
Thus, a final substitution into Eq:
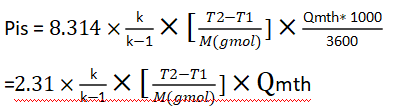
Some other points to note:
- Compressor efficiency. Nowadays, the compressor efficiency is generally between 0.8~0.95, and the following screenshot takes the range of values referenced from “Principles and Structural Design of Displacement Compressors“.
| types | Micro | Small | Medium and large | High Pressure Circulator | Motorcycle compressor |
| η | 0.80~0.87 | 0.85~0.90 | 0.90~0.95 | 0.80~0.85 | 0.85~0.95 |
- Isentropic coefficient (k). You can refer to the calculation table on the right to select the value. It will allow you to calculate the approximate required compressor power and discharge temperature.
| Gas | Isentropic coefficient(k) |
| Acetylene | 1.30 |
| Air, standard condition | 1.40 |
| Ammonia | 1.32 |
| Argon | 1.66 |
| Benzene | 1.12 |
| n-Butane | 1.18 |
| Isobutane | 1.19 |
| Carbon Dioxide | 1.28 |
| Carbon disulfide | 1.21 |
| Carbon monoxide | 1.40 |
| Chlorine | 1.33 |
| Ethane | 1.18 |
| Hydrogen | 1.40 |
| Methane | 1.31 |
- In the case of centrifugal compressors, the isentropic coefficient (k) needs to be replaced by n (polytropic coefficient), which is usually slightly larger than k.
Several Examples
Case 1
A compressor needs to deliver 200Nm³/h of hydrogen at 10 bar, with an inlet gas temperature of 20°C and an inlet pressure of atmospheric pressure. The efficiency of the compressor is known and is 0.85.
The volume flow rate of the compressor is 200Nm³/h, and the specific gravity of hydrogen is 0.089kg/m³ at standard conditions (i.e. 0°C and atmospheric pressure), so the mass flow rate is 200*0.089=17.8kg/h.
In the case of isentropic compression, the exhaust temperature can be calculated using the following equation:
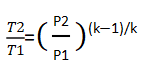
Here, Tdischarge= (20+273.15)*((101325+10*100000)/101325)^((1.4-1)/1.4) =579.6K
579.6 – 273.15 = 306.45°C
Using the simplified equation above:
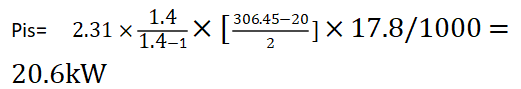
In the last step, we need to consider the compressor’s efficiency, so the power of the compressor= 20.6/0.85 = 24.2kW.
Case 2
A natural gas (methane) compressor needs to deliver 100Nm³/h at 200 bar, with an inlet gas temperature of 20°C and an inlet pressure of 10 bar. The efficiency of the compressor is known and is 0.90.
The volume flow rate of the compressor is 100Nm³/h. Under standard conditions (i.e. 0°C and atmospheric pressure), the specific gravity of methane is 0.716kg/m³, so the mass flow rate is 100*0.716=71.6kg/h.
In the case of isentropic compression, the exhaust temperature can be calculated using the following equation:
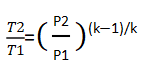
Here, Tdischarge= (20+273.15)*((101325+200*100000)/(101325+10*100000))^((1.3-1)/1.3) =573K
573 – 273.15 = 299.85°C
Using the simplified formula above:
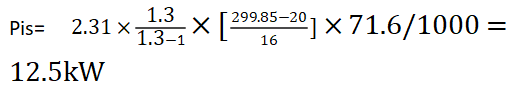
In the last step, we need to take into account the efficiency of the compressor, so the power of the compressor = 12.5/0.9 = 13.9kW
Conclusion
Finally, the above calculations are for reference only, and we do not guarantee the authority of the results. If you need to purchase a compressor for your industry, please consult our engineers for all the details you may need for your design.





 Email
Email sales:+86 15366749631
sales:+86 15366749631

